
Our custom-built Shack-Hartmann wavefront sensor.
Current Projects Related to Image Quality in the Human Eye
Aberrations and Accommodation (coming soon)
Aberrations and Eye Development (coming soon)
Shack-Hartmann Wavefront Sensing
Since Junzhong Liang's published paper on the first application of Shack-Hartmann wavefront sensing for the human eye in 1994 (Liang, Bille, .....), the Shack-Hartmann technique has gained tremendous popularity for both clinical and basic science. The wavefront sensor is a device that is used to measure the aberrations of the eye. As a standalone instrument, it is used to measure refractive errors and high-order aberrations. It can also be used as feedback for aberration correction using adaptive optics, contact lenses or laser refractive surgery. For more information on wavefront sensing, link to talks and tutorials on the International Congress on Wavefront Sensing and Aberration-free Refractive Surgery website.

Our custom-built Shack-Hartmann wavefront sensor.
Screen shots of the main screen and optical performance screen.

![]()
The perception of blur due to monochromatic aberrations.
Brent Wilson and Keith Decker
Aberrations in the human eye cause the defocused point spread function on the retina to appear different depending on whether it is focused in front of behind the retina. (In the eye with no aberrations, they appear essentially the same). Our question was.. How well can the eye use information in the monochromatic PSF to discriminate the direction of defocus?

PSFs calculated from the measured aberrations of one subject. When
the pupil size is small, aberrations are minimal and the PSF for positive
or negative defocus appear the same. When the pupil is large, the aberrations
cause the PSF for positive or negative defocus to appear different. This
work was presented at ARVO, 2000 is published in JOSA A.
3-dimensional Modeling of the Point Spread Function.
Bill Donnelly
The point spread function can be calculated in 3 dimensions. The narrowness of the PSF in the lateral dimension governs the lateral resolution. The axial extent of the PSF near the focal plane governs properties like depth of focus and potential axial resolution in instruments like the Scanning Laser Ophthalmoscope. It is well known that the optimal pupil size for lateral resolution is between 2 and 3 mm. Our question was...What is the optimal pupil size for axial resolution?
To calculate the best pupil size for axial resolution, we measured the wavefront aberrations of 16 eyes and calculated their 3-D PSFs. Axial resolution was computed as the full-width at half-max of the intensity that would be detected in a confocal scanning laser ophthalmoscope if a diffuse object were moved axially through the focal plane of the aberrated objective lens (In a scanning laser ophthalmoscope, the objective lens is the optics of the eye). We determined that the pupil size that gives the narrowest optical section varies greatly between individuals and on average is about 4 mm, which is greater than for optimal lateral resolution.
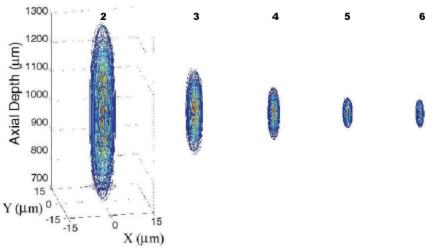
Figure 1: 3-D PSFs for a diffraction-limited eye for pupil sizes from 2 to 6 mm in 1 mm steps.
The relative amount of detected light from scattering points near the best focus in a confocal scanning laser ophthalmoscope varies as the square of the 3-D point spread function. The above figure shows a detail around the focus of the square of a 3-D PSF for a diffraction-limited eye. As the pupil size increases, the light focuses to a smaller and smaller volume, thereby increasing both axial and lateral resolution.
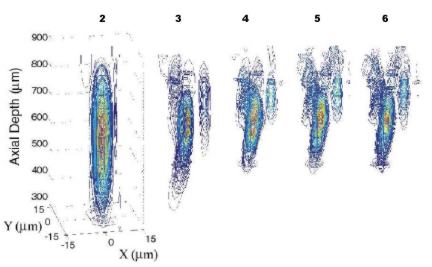
Figure 2: 3-D PSFs for a typical (aberrated) eye for pupil sizes from 2 to 6 mm in 1 mm steps.
In a typical eye, the square of the 3-D PSF gets smaller to a point, but then increases in size again due to the eye's aberrations. In this case, the most compact (3-D PSF)2 occurs for a pupil size of about 3 mm.
last updated: Feb 3, 2005